Cos Pro Python 1급 1차 05번 문제풀이

Contents of table:

• 문제내용
• 정답코드

---

Topic:
소용돌이 수

Review:
유명한 소용돌이 알고리즘 문제이다. 2차원 리스트 안에서, 원하는 대로 point 이동 알고리즘을 짤 수 있는가를 테스트하는 문제이다.

정답코드

---

def in_range(i, j, n): # i와 j값이 0보다크고 n보다 작은지 확인 
    return 0 <= i and i < n and 0 <= j and j < n

def solution(n):
    pane = [[0 for j in range(n)] for i in range(n)] # n * n 크기의 panel 을 만든다.
    dy = [0, 1, 0, -1] # 2차원 리스트 panel 에서, (dy,dx)의 움직임은, (right, down, left, up)을 의미한다.  
    dx = [1, 0, -1, 0]
    ci, cj = 0, 0 # 시작 포인트는 (0,0)
    num = 1
    while in_range(ci, cj, n) and pane[ci][cj] == 0: # 1) in_range 함수를 활용, current point가 panel을 벗어나지 않음. 2) 이동하는 칸에 숫자가 채워져 있지 않음.
        for k in range(4): # dy, dx의 이동순서 
            if not in_range(ci, cj, n) or pane[ci][cj] != 0:
                break
            while True: # 1) pannel 범위안 2) 다음칸의 숫자가 비어있을 때, 무한루프 
                pane[ci][cj] = num # k = 0 일 때, panel의 범위 안에서 num +=1 만큼의 숫자를 각 칸에 입력            
                num += 1  
                ni = ci + dy[k] # next point는 current point 에서 (dy,dx) 만큼의 이동값을 가져간 결과이다. 
                nj = cj + dx[k] 
                if not in_range(ni, nj, n) or pane[ni][nj] != 0: # next point 가 pannel 을 벗어났을 경우, (down, left, up, right) 순서로 이동.  
                    ci += dy[(k + 1) % 4] # (k+1) % 4 는 1 2 3 0 
                    cj += dx[(k + 1) % 4]
                    break
                ci = ni 
                cj = nj
    return pane

문제내용

#문제5
다음과 같이 n x n 크기의 격자에 1부터 n x n까지의 수가 하나씩 있습니다.

이때 수가 다음과 같은 순서로 배치되어있다면 이것을 n-소용돌이 수라고 부릅니다.

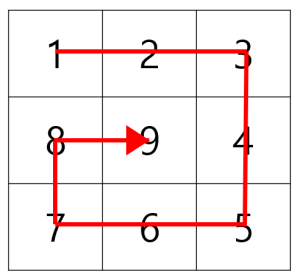
소용돌이 수에서 1행 1열부터 n 행 n 열까지 대각선상에 존재하는 수들의 합을 구해야 합니다.

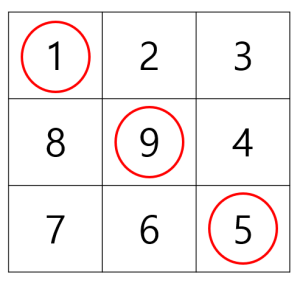
위의 예에서 대각선상에 존재하는 수의 합은 15입니다.
격자의 크기 n이 주어질 때 n-소용돌이 수의 대각선상에 존재하는 수들의 합을 return 하도록 solution 함수를 완성해주세요.

---

매개변수 설명

격자의 크기 n이 solution 함수의 매개변수로 주어집니다.

• n은 1 이상 100 이하의 자연수입니다.

---

return 값 설명

n-소용돌이 수의 대각선상에 존재하는 수들의 합을 return 해주세요.

---

예시

n	return
3	15
2	4

예시 설명

예시 #1
문제의 예와 같습니다.

예시 #2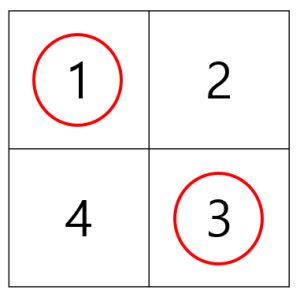

1과 3을 더하여 4가 됩니다.